LOS SISTEMAS NUMÉRICOS Y ALFABÉTICOS
Un sistema de numeración es un
conjunto de símbolos y reglas de generación que permiten construir todos los
números válidos.
En un sistema de numeración es
importante distinguir la base, que es el número de símbolos que utiliza y que
se caracteriza por ser el coeficiente que determina cual es el valor de cada
símbolo.
Los sistemas de numeración
actuales son sistemas posicionales, en los que el valor relativo que representa
cada símbolo, o cifra, depende de su valor absoluto y de la posición relativa
que ocupa dicha cifra con respecto a la coma decimal, íntimamente ligada al
valor de la base del sistema de numeración empleado.
SISTEMAS DE NUMERACIÓN
Binario (base 2): 0, 1
Octal (base 8): 0, 1, 2, 3, 4, 5, 6, 7
Decimal (base 10): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Hexadecimal (base 16): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
EJEMPLOS DE CONVERCIÓN Tabla de conversión:
| Binario | Octal | Decimal | Hexadecimal |
|---|---|---|---|
| 0000 | 0 | 0 | 0 |
| 0001 | 1 | 1 | 1 |
| 0010 | 2 | 2 | 2 |
| 0011 | 3 | 3 | 3 |
| 0100 | 4 | 4 | 4 |
| 0101 | 5 | 5 | 5 |
| 0110 | 6 | 6 | 6 |
| 0111 | 7 | 7 | 7 |
| 1000 | 10 | 8 | 8 |
| 1001 | 11 | 9 | 9 |
| 1010 | 12 | 10 | A |
| 1011 | 13 | 11 | B |
| 1100 | 14 | 12 | C |
| 1101 | 15 | 13 | D |
| 1110 | 16 | 14 | E |
| 1111 | 17 | 15 | F |
CONVERSIONES
DECIMAL
DECIMAL A BINARIO
Para hacer la conversión de decimal a binario, hay que ir
dividiendo el número decimal entre dos y anotar en una columna a la derecha el
resto (un 0 si el resultado de la división es par y un 1 si es impar).
La lista de ceros y unos leídos de abajo a arriba es el
resultado.
PROCEDIMIENTO
- Dividir entre 2 sucesivamente.
- Apuntar el resultado y el resto de cada operación.
-Apuntar a lista de ceros y unos de abajo a arriba.
DECIMAL A OCTAL
PROCEDIMIENTO
-Se basa en dividir entre 8 el número decimal.
-Anotar el resto y continuar dividendo el cociente obtenido
entre ocho sucesivamente, En este proceso se crea una cadena de números con los
restos de las divisiones y el cociente de la división final, estos valores
numéricos serán de entre 7 y 0,
-Se ordenan de derecha a izquierda y de esta forma se
obtiene el número octal correspondiente al número decimal.
DECIMAL A HEXADECIMAL
-Se realiza dividiendo entre 16 el número decimal que queremos convertir tratando la división como una división entera sin decimales.
-anotar el resto y continuar dividendo el
cociente obtenido entre dieciséis hasta conseguir un cociente final de entre 1
y 15.
-Logrando una secuencia de
numero decimales con los restos de cada división y el cociente final, que
sustituiremos por el equivalente hexadecimal de la tabla de más arriba, y se ordenan de abajo hacia arriba
BINARIO
BINARIO A DECIMAL
-Se escribe las potencias de DOS (2) de derecha a izquierda debajo del número binario, dándole a la primera potencia 20 el valor UNO (1).
-Llegados a este punto anotaremos el resultado de la potencia correspondiente al dígito binario multiplicando este por su valor (0 o 1), es decir, si por ejemplo «El tercer dígito del número binario empezando por la derecha es UNO (1), multiplicaremos UNO (1) por la potencia de 22 y lo anotaremos».
Nota: Recuerda que el primer dígito empezando por la
derecha tiene una potencia de 20 que deduciremos su valor por UNO (1) si el
valor binario es UNO (1) y CERO (0) si el valor del numero binario es CERO (0).
BINARIO A OCTAL
PROCEDIMIENTO
-Se basa en empezar por separar el número binario en
bloques de TRES (3) dígitos empezando desde la derecha hasta la izquierda,
quedando tal que así:
BINARIO A HEXADECIMAL
PROCEDIMIENTO
-Se basa en empezar por separar el número binario en
bloques de 4 dígitos empezando desde la derecha hasta la izquierda, quedando
tal que así:
-con la ayuda de la tabla de conversión roja de arriba, se
sustituye cada bloque de dígitos binarios por su correspondiente equivalente en
hexadecimal.
OCTAL
OCTAL A DECIMAL
Se basa en multiplicar cada dígito del número
octal por el numero decimal equivalente resudado de la potencia correspondiente
según la posición de dicho dígito en el número.
-Se escribe las potencias de OCHO (8) de derecha
a izquierda debajo de cada dígito de nuestro número octal, dándole a la primera
potencia 80 el valor UNO (1).
-Luego se escribe el resultado de las potencias de base OCHO
(8) y se multiplica cada uno de ellos por el dígito octal superior, quedando
una cadena de productos que se suma para finalmente obtener el equivalente número
decimal del número octal.
Nota: Recuerda que el primer dígito empezando por la
derecha tiene una potencia de 80 que deduciremos su valor por UNO (1).
OCTAL A BINARIO
PROCEDIMIENTO
-Se basa en sustituir cada dígito del número octal por los
TRES (3) dígitos binarios que le corresponden.
Nota: En la tabla de más arriba puedes ver la equivalencia
binaria para cada uno de los posibles dígitos de tu número octal.
En este proceso se ha creado una cadena de valores numéricos
de CEROS (0) y UNOS (1) que al agruparlos (y eliminando los ceros de la
izquierda en caso de que existan) se obtiene el número binario correspondiente
al número octal.
OCTAL A HEXADECIMAL
PROCEDIMIENTO
El primer paso para convertir un numero octal en
hexadecimal es convertir el número octal en binario, para ello, nos ayudaremos
de la tabla conversora de octal a binario y se traduce el número
octal escribiendo debajo de cada dígito la correspondencia en binario.
Obtenido el número binario se realiza la conversión de binario a hexadecimal, empezando por separar el número binario en bloques de 4 dígitos empezando desde la derecha hasta la izquierda, luego con la ayuda de la tabla de conversión binario a hexadecimal se sustituye cada bloque de dígitos binarios por su correspondiente equivalente en hexadecimal.
HEXADECIMAL
HEXADECIMAL A DECIMAL
Se basa en ir reemplazando cada dígito del número
hexadecimal por el equivalente número decimal según la posición de dicho dígito
hexadecimal en el número, multiplicar este por la potencia de DIECISÉIS (16)
correspondiente a cada uno de ellos y sumar todo.
PROCEDIMIENTO
1. Primero se debe escribir debajo de cada dígito hexadecimal
el numero decimal equivalente con la ayuda de la tabla de conversión de más
arriba.
2. luego escribir debajo de cada valor decimal obtenido la
potencia con base de DIECISÉIS (16) correspondiente de derecha a izquierda,
dándole a la primera potencia 160 el valor UNO (1).
3. Por último se multiplica cada valor decimal por la potencia de DIECISÉIS (16) correspondiente a cada posición, se anota el producto de todas las multiplicaciones y cuando termine el proceso se suma los resultados.
Nota: Recuerda que el primer dígito empezando por la
derecha tiene una potencia de 160 que deduciremos su valor por UNO (1).
HEXADECIMAL A BINARIO
PROCEDIMIENTO
Se basa tan solo en sustituir cada dígito del número
hexadecimal por los CUATRO (4) dígitos binarios que le corresponden.
Nota: En la tabla de más arriba puedes ver la equivalencia
binaria para cada uno de los posibles dígitos de tu numero hexadecimal.
En este proceso se crea una cadena de valores numéricos de
CEROS (0) y de UNOS (1) que al agruparlos (y eliminando los ceros de la
izquierda en caso de que existan) se obtiene el numero binario correspondiente
al número hexadecimal.
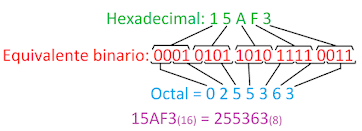
HEXADECIMAL A OCTAL
PROCEDIMIENTO
El primer paso para convertir un número hexadecimal en
octal es convertir el numero hexadecimal a binario, para ello, nos ayudaremos
de la tabla conversora hexadecimal a binario de arriba y traduciremos el numero
hexadecimal escribiendo debajo de cada dígito la correspondencia en binario.
Obtenido el numero binario se realiza la conversión de
binario a octal, empezando por separar el numero binario en bloques de 3 dígitos
empezando desde la derecha hasta la izquierda, tomaremos ayuda de la tabla de
conversión binario a octal que hemos visto más arriba y sustituiremos cada
bloque de dígitos binarios por su correspondiente equivalente en octal.
REFERENCIAS
https://elpuig.xeill.net/Members/vcarceler/c1/didactica/apuntes/ud1/na3
http://recursostic.educacion.es/secundaria/edad/4esotecnologia/quincena5/4q2_contenidos_2c.htm























No hay comentarios:
Publicar un comentario